CS788 Assignment 1

	Billy Biggs 97049311
	wbiggs@uwaterloo.ca

Problem 1: Raytracer

I'm submitting a rewrite of my path tracer. This version supports: I use optimized intersection source code from: 
  Haines, Eric, "Point in Polygon Strategies," Graphics Gems IV, ed.
  Paul Heckbert, Academic Press, p. 24-46, 1994
  http://www.acm.org/pubs/tog/editors/erich/ptinpoly/.

  Tomas Möller and Ben Trumbore., "Fast, minimum storage ray-triangle intersection."
  Journal of Graphics Tools, 2(1):21--28, 1997. 
  http://www.graphics.cornell.edu/pubs/1997/MT97.html.
The adaptive supersampling technique is taken from Foly & van Dam. My reference for colour and gamma functions is, as always, Poynton. The model of the teapot is from an example nVidia model, and the phone handset (yes, that's what it is) is from an unknown source.

Source code and executable for the raytracer is here.

My scene: Flying teapot, blue sphere, and flying phone handset. Teapot model has over 8400 polygons. 2x supersampled. Two point light sources. Phong exponent of 50. (Yes, I'm going to code vertex normal support next, just to make that teapot look better).
My scene with vertex normals: Flying teapot, blue sphere, and flying phone handset. No vertex normals for the flying phone handset because of the silly model format used to generate it. This code was not in the raytracer I submitted for assignment 1, and I just put this up here because it's a cool contrast to the image above.

Problem 2: sRGB Conversion Matrix

The colour primaries used are defined in xyY space.

Red $x = 0.640$ $y = 0.330$
Green $x = 0.300$ $y = 0.600$
Blue $x = 0.150$ $y = 0.060$
White (D65) $x = 0.3127$ $y = 0.3290$


These are the primaries specified by both ITU-R BT.709 and sRGB. Given these chromanicities, we are given a relationship between the $XYZ$ coordinates and the values of $R$, $G$, and $B$. For example, the $X$ value of any $RGB$ colour can be expressed as a linear combination of the $X$ values for $R$, $G$, and $B$ individually. Since we can derive those from the chromanicities, we define constants $C_r$, $C_g$ and $C_g$ to represent the factors of which the chromanicities contribute to the resulting $XYZ$ value. To solve these values, I'm using the notation and ideas from the method described in Foley/van Dam.

\begin{eqnarray*} \left[\begin{array}{c} X \\ Y \\ Z \\ \end{array}\right] & = &... ...ft[\begin{array}{c} R \\ G \\ B \\ \end{array}\right] \end{array}\end{eqnarray*}



In order to compute the values of $C_r$, $C_g$ and $C_b$, we need a known reference point. For this we will use the D65 white point (black body at 6500K) and use unity luminance ($Y$) and map this to $R = G = B = 1$.

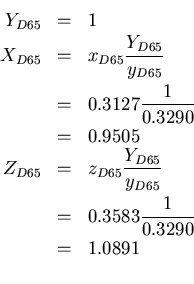
\begin{eqnarray*} Y_{D65} &=& 1 \\ X_{D65} &=& x_{D65} \frac{Y_{D65}}{y_{D65}} ... ...}}{y_{D65}} \\ &=& 0.3583 \frac{1}{0.3290} \\ &=& 1.0891 \\ \end{eqnarray*}



We can now use these to solve for $C_r$, $C_g$ and $C_b$ by taking the inverse of the following:

\begin{eqnarray*} \left[\begin{array}{c} X_{D65} \\ Y_{D65} \\ Z_{D65} \\ \end{a... ...gin{array}{c} C_r \\ C_g \\ C_b \\ \end{array}\right] \end{array}\end{eqnarray*}



We get:

\begin{eqnarray*} \left[\begin{array}{c} C_r \\ C_g \\ C_b \\ \end{array}\right]... ...n{array}{c} 0.6444 \\ 1.1919 \\ 1.2033 \\ \end{array}\right] \\ \end{eqnarray*}



Submitting back, we get the final matrix:

\begin{eqnarray*} \left[\begin{array}{c} X \\ Y \\ Z \\ \end{array}\right] & = &... ...ft[\begin{array}{c} R \\ G \\ B \\ \end{array}\right] \end{array}\end{eqnarray*}



Inverting this we get the desired matrix:

\begin{eqnarray*} \left[\begin{array}{c} R_{sRGB} \\ G_{sRGB} \\ Z_{sRGB} \\ \en... ...egin{array}{c} X \\ Y \\ Z \\ \end{array}\right] \end{array} \\ \end{eqnarray*}



Problem 3: sRGB Matching Functions

The matching functions are created by converting the xbar, ybar and zbar quantities to sRGB-space.
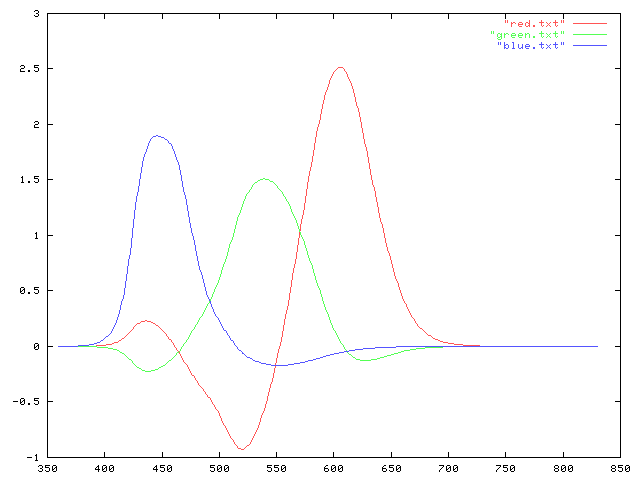
Raw version, relative sensitivity on the y axis, wavelength in nanometers along the x axis.
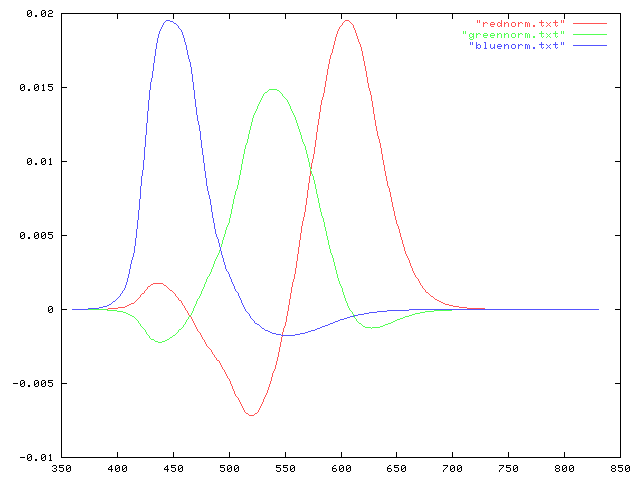
Normalized version such that each integral sums to unity. Again, relative sensitivity on the y axis, wavelength in nanometers along the x axis.

Problem 4: Chromaticity Diagrams

The horseshoe-shape is created by mapping spikes at each wavelength into xy coordinates. I then create a convex polygon out of the points and test xy coordinates to ensure they are within the polygon using the intersection routine I found for my raytracer. Out of gamut colours are handled by desaturating towards our mapping for D65 white (the white point of sRGB). In each image, the white point is marked by a white pixel, as is each wavelength reference point. Each image is generated as RGB values mapped into gamut (values larger than 0) and then scanned to find the largest component value. When this is found, all colours are scaled such that the largest value maps to 1.0, at which point the image is gamma corrected and output.

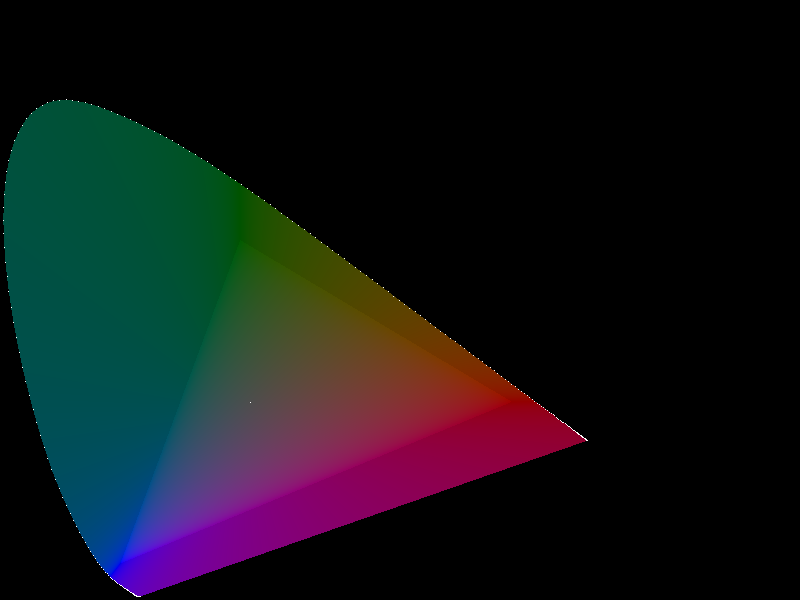
Plot of xy chromaticities with the sRGB gamut hilighted by slightly higher luminance. x values along the x axis, y values along the y axis, with 0,0 in the lower left corner of the image. This image was converted to sRGB for a display gamma of 2.2 (using the crazy 2.4 curve specified in the standard).

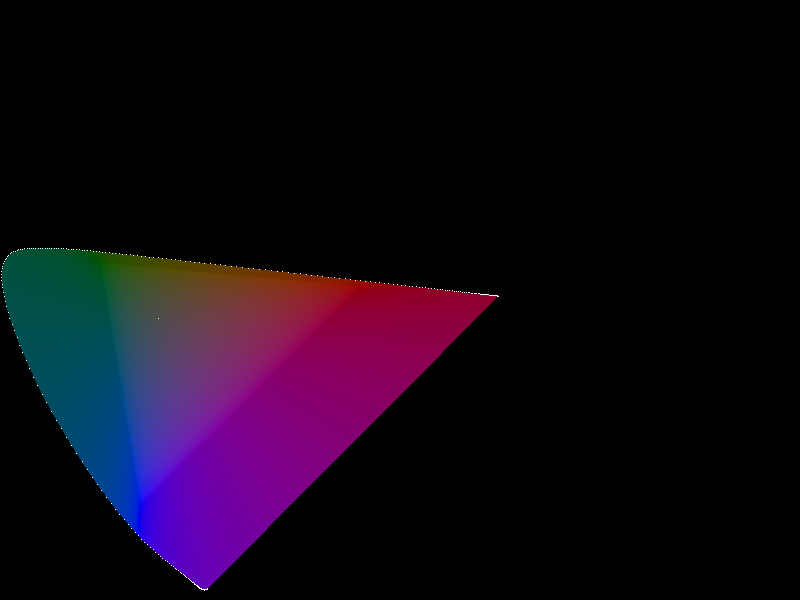
Plot of u'v' chromaticities with the sRGB gamut hilighted by slightly higher luminance. The u' axis is along the bottom, and the v' axis along the left so 0,0 is again in the lower left corner. This image was also corrected for a display gamma of 2.2.
[ICO]NameLast modifiedSizeDescription
[PARENTDIR]Parent Directory   -  
[TXT]final.txt 2002-01-30 05:44 324K 
[ ]submission.tar.gz 2002-01-30 05:53 307K 
[ ]portray-0.1.tar.gz 2002-01-30 00:23 154K 
[ ]srgb-derivation.ps 2002-01-30 05:32 78K 
[IMG]xy-srgb-ymapped.png 2002-01-30 15:49 60K 
[IMG]xy-srgb.png 2002-01-29 21:43 48K 
[IMG]spheres.png 2002-01-29 23:18 41K 
[IMG]uv-srgb.png 2002-01-29 21:43 35K 
[IMG]final.png 2002-01-30 05:16 30K 
[IMG]final-vnormals.png 2002-01-30 23:46 27K 
[ ]colour-0.1.tar.gz 2002-01-30 05:53 18K 
[TXT]textonly.html 2002-01-30 00:09 9.0K 
[IMG]img23.png 2002-01-30 00:04 6.0K 
[IMG]img24.png 2002-01-30 00:04 4.8K 
[IMG]rgbnorm.png 2002-01-29 21:42 4.6K 
[IMG]rgbraw.png 2002-01-29 21:42 4.4K 
[ ]srgb-derivation.tex 2002-01-30 00:06 3.7K 
[IMG]img21.png 2002-01-30 00:04 3.7K 
[IMG]img17.png 2002-01-30 00:04 3.2K 
[IMG]img22.png 2002-01-30 00:04 3.0K 
[IMG]img8.png 2002-01-30 00:04 610  
[IMG]img2.png 2002-01-30 00:04 561  
[IMG]img20.png 2002-01-30 00:04 555  
[IMG]img4.png 2002-01-30 00:04 533  
[IMG]img7.png 2002-01-30 00:04 531  
[IMG]img6.png 2002-01-30 00:04 531  
[IMG]img1.png 2002-01-30 00:04 497  
[IMG]img3.png 2002-01-30 00:04 479  
[IMG]img5.png 2002-01-30 00:04 473  
[IMG]img14.png 2002-01-30 00:04 438  
[IMG]img9.png 2002-01-30 00:04 409  
[IMG]img16.png 2002-01-30 00:04 332  
[IMG]img18.png 2002-01-30 00:04 327  
[IMG]img15.png 2002-01-30 00:04 313  
[IMG]img11.png 2002-01-30 00:04 271  
[IMG]img10.png 2002-01-30 00:04 270  
[IMG]img12.png 2002-01-30 00:04 260  
[IMG]img13.png 2002-01-30 00:04 255  
[IMG]img19.png 2002-01-30 00:04 245  
[DIR]colour/ 2002-01-29 23:21 -