Billy Biggs 97049311 wbiggs@uwaterloo.ca
| Red | ||
| Green | ||
| Blue | ||
| White (D65) |
These are the primaries specified by both ITU-R BT.709 and sRGB. Given
these chromanicities, we are given a relationship between the ![]() coordinates and the values of
coordinates and the values of ![]() ,
, ![]() , and
, and ![]() . For example, the
. For example, the ![]() value of any
value of any ![]() colour can be expressed as a linear combination of
the
colour can be expressed as a linear combination of
the ![]() values for
values for ![]() ,
, ![]() , and
, and ![]() individually. Since we can derive
those from the chromanicities, we define constants
individually. Since we can derive
those from the chromanicities, we define constants ![]() ,
, ![]() and
and
![]() to represent the factors of which the chromanicities contribute to
the resulting
to represent the factors of which the chromanicities contribute to
the resulting ![]() value. To solve these values, I'm using the
notation and ideas from the method described in Foley/van Dam.
value. To solve these values, I'm using the
notation and ideas from the method described in Foley/van Dam.
![\begin{eqnarray*}
\left[\begin{array}{c} X \\ Y \\ Z \\ \end{array}\right]
& = &...
...ft[\begin{array}{c} R \\ G \\ B \\ \end{array}\right]
\end{array}\end{eqnarray*}](img17.png)
In order to compute the values of ![]() ,
, ![]() and
and ![]() , we need a
known reference point. For this we will use the D65 white point (black
body at 6500K) and use unity luminance (
, we need a
known reference point. For this we will use the D65 white point (black
body at 6500K) and use unity luminance (![]() ) and map this to
) and map this to ![]() .
.
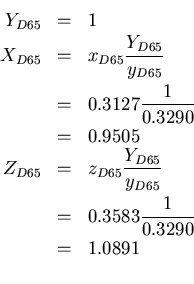
We can now use these to solve for ![]() ,
, ![]() and
and ![]() by taking the
inverse of the following:
by taking the
inverse of the following:
![\begin{eqnarray*}
\left[\begin{array}{c} X_{D65} \\ Y_{D65} \\ Z_{D65} \\ \end{a...
...gin{array}{c} C_r \\ C_g \\ C_b \\ \end{array}\right]
\end{array}\end{eqnarray*}](img22.png)
We get:
![\begin{eqnarray*}
\left[\begin{array}{c} C_r \\ C_g \\ C_b \\ \end{array}\right]...
...n{array}{c} 0.6444 \\ 1.1919 \\ 1.2033 \\ \end{array}\right] \\
\end{eqnarray*}](img23.png)
Submitting back, we get the final matrix:
![\begin{eqnarray*}
\left[\begin{array}{c} X \\ Y \\ Z \\ \end{array}\right]
& = &...
...ft[\begin{array}{c} R \\ G \\ B \\ \end{array}\right]
\end{array}\end{eqnarray*}](img17.png)
Inverting this we get the desired matrix:
![\begin{eqnarray*}
\left[\begin{array}{c} R_{sRGB} \\ G_{sRGB} \\ Z_{sRGB} \\ \en...
...egin{array}{c} X \\ Y \\ Z \\ \end{array}\right]
\end{array} \\
\end{eqnarray*}](img24.png)
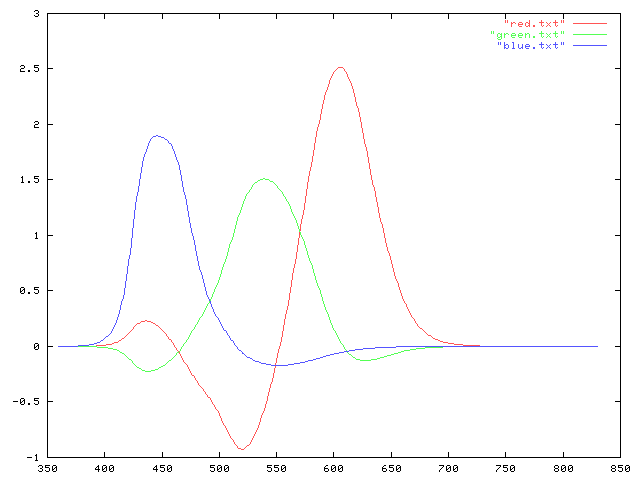
|
| Raw version, relative sensitivity on the y axis, wavelength in nanometers along the x axis. |
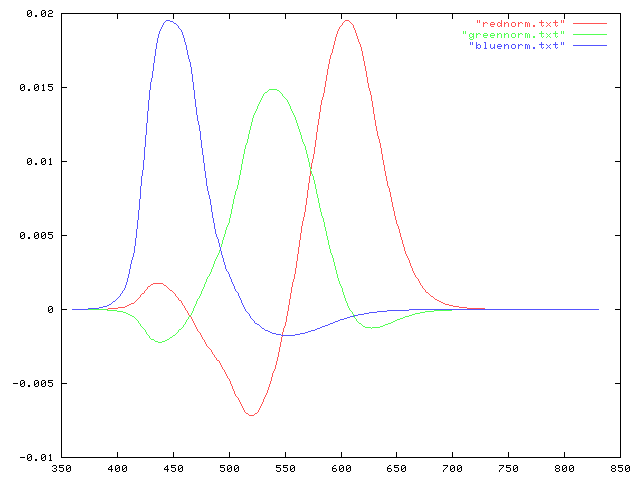
|
| Normalized version such that each integral sums to unity. Again, relative sensitivity on the y axis, wavelength in nanometers along the x axis. |